Ideal Operational Amplifiers
As well as resistors and capacitors, Operational Amplifiers, or Op-amps as they are more commonly called, are one of the basic building blocks of Analogue Electronic Circuits. Operational amplifiers are linear devices that have all the properties required for nearly ideal DC amplification and are therefore used extensively in signal conditioning, filtering or to perform mathematical operations such as add, subtract, integration and differentiation. An ideal Operational Amplifier is basically a three-terminal device which consists of two high impedance inputs, one called the Inverting Input, marked with a negative or "minus" sign, ( "-" ) and the other one called the Non-inverting Input, marked with a positive or "plus" sign ( "+" ).
The third terminal represents the op-amps output port which can both sink and source either a voltage or a current. In a linear operational amplifier, the output signal is the amplification factor, known as the amplifiers gain ( A ) multiplied by the value of the input signal and depending on the nature of these input and output signals, there can be four different classifications of operational amplifier gain.
- Voltage – Voltage "in" and Voltage "out"
- Current – Current "in" and Current "out"
- Transconductance – Voltage "in" and Current "out"
- Transresistance – Current "in" and Voltage "out"
Since most of the circuits dealing with operational amplifiers are voltage amplifiers, we will limit the tutorials in this section to voltage amplifiers only, (Vin and Vout).
The amplified output signal of an Operational Amplifier is the difference between the two signals being applied to the two inputs. In other words the output signal is a differential signal between the two inputs and the input stage of an Operational Amplifier is in fact a differential amplifier as shown below.
Differential Amplifier
The circuit below shows a generalized form of a differential amplifier with two inputs marked V1 and V2. The two identical transistors TR1 and TR2 are both biased at the same operating point with their emitters connected together and returned to the common rail, -Vee by way of resistor Re.
Differential Amplifier
The circuit operates from a dual supply+Vcc and -Vee which ensures a constant supply. The voltage that appears at the output, Vout of the amplifier is the difference between the two input signals as the two base inputs are in anti-phase with each other. So as the forward bias of transistor,TR1 is increased, the forward bias of transistor TR2 is reduced and vice versa. Then if the two transistors are perfectly matched, the current flowing through the common emitter resistor, Re will remain constant.
Like the input signal, the output signal is also balanced and since the collector voltages either swing in opposite directions (anti-phase) or in the same direction (in-phase) the output voltage signal, taken from between the two collectors is, assuming a perfectly balanced circuit the zero difference between the two collector voltages. This is known as the Common Mode of Operation with the common mode gain of the amplifier being the output gain when the input is zero.
Ideal Operational Amplifiers also have one output (although there are ones with an additional differential output) of low impedance that is referenced to a common ground terminal and it should ignore any common mode signals that is, if an identical signal is applied to both the inverting and non-inverting inputs there should no change to the output. However, in real amplifiers there is always some variation and the ratio of the change to the output voltage with regards to the change in the common mode input voltage is called the Common Mode Rejection Ratio or CMRR.
Operational Amplifiers on their own have a very high open loop DC gain and by applying some form ofNegative Feedback we can produce an operational amplifier circuit that has a very precise gain characteristic that is dependant only on the feedback used. An operational amplifier only responds to the difference between the voltages on its two input terminals, known commonly as the "Differential Input Voltage" and not to their common potential. Then if the same voltage potential is applied to both terminals the resultant output will be zero. An Operational Amplifiers gain is commonly known as theOpen Loop Differential Gain, and is given the symbol (Ao).
Equivalent Circuit for Ideal Operational Amplifiers
Op-amp Idealized Characteristics
| PARAMETER | IDEALIZED CHARACTERISTIC |
| Open Loop Gain, (Avo) | Infinite - The main function of an operational amplifier is to amplify the input signal and the more open loop gain it has the better. Open-loop gain is the gain of the op-amp without positive or negative feedback and for an ideal amplifier the gain will be infinite but typical real values range from about 20,000 to 200,000. |
| Input impedance, (Zin) | Infinite - Input impedance is the ratio of input voltage to input current and is assumed to be infinite to prevent any current flowing from the source supply into the amplifiers input circuitry (Iin =0). Real op-amps have input leakage currents from a few pico-amps to a few milli-amps. |
| Output impedance, (Zout) | Zero - The output impedance of the ideal operational amplifier is assumed to be zero acting as a perfect internal voltage source with no internal resistance so that it can supply as much current as necessary to the load. This internal resistance is effectively in series with the load thereby reducing the output voltage available to the load. Real op-amps have output-impedance in the 100-20Ω range. |
| Bandwidth, (BW) | Infinite - An ideal operational amplifier has an infinite frequency response and can amplify any frequency signal from DC to the highest AC frequencies so it is therefore assumed to have an infinite bandwidth. With real op-amps, the bandwidth is limited by the Gain-Bandwidth product (GB), which is equal to the frequency where the amplifiers gain becomes unity. |
| Offset Voltage, (Vio) | Zero - The amplifiers output will be zero when the voltage difference between the inverting and the non-inverting inputs is zero, the same or when both inputs are grounded. Real op-amps have some amount of output offset voltage. |
From these "idealized" characteristics above, we can see that the input resistance is infinite, so no current flows into either input terminal (the "current rule") and that the differential input offset voltage is zero (the "voltage rule"). It is important to remember these two properties as they will help us understand the workings of the Operational Amplifier with regards to the analysis and design of op-amp circuits.
However, real Operational Amplifiers such as the commonly available uA741, for example do not have infinite gain or bandwidth but have a typical "Open Loop Gain" which is defined as the amplifiers output amplification without any external feedback signals connected to it and for a typical operational amplifier is about 100dB at DC (zero Hz). This output gain decreases linearly with frequency down to "Unity Gain" or 1, at about 1MHz and this is shown in the following open loop gain response curve.
Open-loop Frequency Response Curve
From this frequency response curve we can see that the product of the gain against frequency is constant at any point along the curve. Also that the unity gain (0dB) frequency also determines the gain of the amplifier at any point along the curve. This constant is generally known as the Gain Bandwidth Product or GBP.
Therefore, GBP = Gain x Bandwidth or A x BW.
For example, from the graph above the gain of the amplifier at 100kHz = 20dB or 10, then the
GBP = 100,000Hz x 10 = 1,000,000.
Similarly, a gain at 1kHz = 60dB or 1000, therefore the
GBP = 1,000 x 1,000 = 1,000,000. The same!.
The Voltage Gain (A) of the amplifier can be found using the following formula:
and in Decibels or (dB) is given as:
An Operational Amplifiers Bandwidth
The operational amplifiers bandwidth is the frequency range over which the voltage gain of the amplifier is above 70.7% or -3dB (where 0dB is the maximum) of its maximum output value as shown below.
Here we have used the 40dB line as an example. The -3dB or 70.7% of Vmax down point from the frequency response curve is given as 37dB. Taking a line across until it intersects with the main GBP curve gives us a frequency point just above the 10kHz line at about 12 to 15kHz. We can now calculate this more accurately as we already know the GBP of the amplifier, in this particular case 1MHz.
Example No1.
Using the formula 20 log (A), we can calculate the bandwidth of the amplifier as:
37 = 20 log A therefore, A = anti-log (37 ÷ 20) = 70.8
GBP ÷ A = Bandwidth, therefore, 1,000,000 ÷ 70.8 = 14,124Hz, or 14kHz
Then the bandwidth of the amplifier at a gain of 40dB is given as 14kHz as previously predicted from the graph.
Example No2.
If the operational amplifiers gain was reduced by half to say 20dB in the above frequency response curve, the -3dB point would now be at 17dB. This would then give us an overall gain of 7.08, therefore A = 7.08. If we use the same formula as above this new gain would give us a bandwidth of 141.2kHz, ten times more than at 40dB. It can therefore be seen that by reducing the overall open loop gain of an operational amplifier its bandwidth is increased and visa versa. The -3dB point is also known as the "half power point", as the output power of the amplifier is at half its maximum value at this point.
Operational Amplifiers Summary
Op-amp Symbol
An "ideal" or perfect Operational Amplifier is a device with certain special characteristics such as infinite open-loop gain Ao, infinite input resistance Rin, zero output resistance Rout, infinite bandwidth 0 to ∞and zero offset (the output is exactly zero when the input is zero).
There are a very large number of operational amplifier IC's available to suit every possible application from standard bipolar, precision, high-speed, low-noise, high-voltage, etc in either standard configuration or with internal JFET transistors. Operational amplifiers are available in IC packages of either single, dual or quad op-amps within one single device. The most commonly available and used of all operational amplifiers in basic electronic kits and projects is the industry standard μA-741.
The Inverting Amplifier
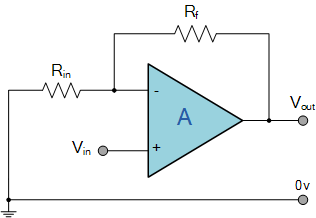
We saw in the last tutorial that the Open Loop Gain, (Avo) of an ideal operational amplifier can be very high, as much as 1,000,000 (120dB) or more. However, this very high gain is of no real use to us as it makes the amplifier both unstable and hard to control as the smallest of input signals, just a few micro-volts, (μV) would be enough to cause the output voltage to saturate and swing towards one or the other of the voltage supply rails losing complete control. As the open loop DC gain of an operational amplifier is extremely high we can therefore afford to lose some of this gain by connecting a suitable resistor across the amplifier from the output terminal back to the inverting input terminal to both reduce and control the overall gain of the amplifier. This then produces and effect known commonly as Negative Feedback, and thus produces a very stable Operational Amplifier based system.
Negative Feedback is the process of "feeding back" a fraction of the output signal back to the input, but to make the feedback negative, we must feed it back to the negative or "inverting input" terminal of the op-amp using an external Feedback Resistor called Rf. This feedback connection between the output and the inverting input terminal forces the differential input voltage towards zero. This effect produces a closed loop circuit to the amplifier resulting in the gain of the amplifier now being called its Closed-loop Gain. A closed-loop amplifier uses negative feedback to accurately control the overall gain but at a cost in the reduction of the amplifiers bandwidth.
This negative feedback results in the inverting input terminal having a different signal on it than the actual input voltage as it will be the sum of the input voltage plus the negative feedback voltage giving it the label or term of a Summing Point. We must therefore separate the real input signal from the inverting input by using an Input Resistor, Rin. As we are not using the positive non-inverting input this is connected to a common ground or zero voltage terminal as shown below, but the effect of this closed loop feedback circuit results in the voltage potential at the inverting input being equal to that at the non-inverting input producing a Virtual Earth summing point because it will be at the same potential as the grounded reference input. In other words, the op-amp becomes a "differential amplifier".
Inverting Amplifier Configuration
In this Inverting Amplifier circuit the operational amplifier is connected with feedback to produce a closed loop operation. For ideal op-amps there are two very important rules to remember about inverting amplifiers, these are: "no current flows into the input terminal" and that "V1 equals V2", (in real op-amps both these rules are broken). This is because the junction of the input and feedback signal (X) is at the same potential as the positive (+) input which is at zero volts or ground then, the junction is a"Virtual Earth". Because of this virtual earth node the input resistance of the amplifier is equal to the value of the input resistor, Rin and the closed loop gain of the inverting amplifier can be set by the ratio of the two external resistors.
We said above that there are two very important rules to remember about Inverting Amplifiers or any operational amplifier for that matter and these are.
- 1. No Current Flows into the Input Terminals
- 2. The Differential Input Voltage is Zero as V1 = V2 = 0 (Virtual Earth)
Then by using these two rules we can derive the equation for calculating the closed-loop gain of an inverting amplifier, using first principles.
Current ( i ) flows through the resistor network as shown.
Then, the Closed-Loop Voltage Gain of an Inverting Amplifier is given as.
and this can be transposed to give Vout as:
and this can be transposed to give Vout as:
 |
| Linear output |
The equation for the output voltage Vout also shows that the circuit is linear in nature for a fixed amplifier gain as Vout = Vin x Gain. This property can be very useful for converting a smaller sensor signal to a much larger voltage.
Another useful application of an inverting amplifier is that of a "transresistance amplifier" circuit. ATransresistance Amplifier also known as a "transimpedance amplifier", is basically a current-to-voltage converter (Current "in" and Voltage "out"). They can be used in low-power applications to convert a very small current generated by a photo-diode or photo-detecting device etc, into a usable output voltage which is proportional to the input current as shown.
Transresistance Amplifier Circuit
The simple light-activated circuit above, converts a current generated by the photo-diode into a voltage. The feedback resistor Rf sets the operating voltage point at the inverting input and controls the amount of output. The output voltage is given as Vout = Is x Rf. Therefore, the output voltage is proportional to the amount of input current generated by the photo-diode.
Example No1
Find the closed loop gain of the following inverting amplifier circuit.
Using the previously found formula for the gain of the circuit
we can now substitute the values of the resistors in the circuit as follows,
Rin = 10kΩ and Rf = 100kΩ.
and the gain of the circuit is calculated as -Rf/Rin = 100k/10k = 10.
therefore, the closed loop gain of the inverting amplifier circuit above is given 10 or 20dB (20log(10)).
Example No2
The gain of the original circuit is to be increased to 40 (32dB), find the new values of the resistors required.
Assume that the input resistor is to remain at the same value of 10KΩ, then by re-arranging the closed loop voltage gain formula we can find the new value required for the feedback resistor Rf.
Gain = -Rf/Rin
therefore, Rf = Gain x Rin
Rf = 40 x 10,000
Rf = 400,000 or 400KΩ
The new values of resistors required for the circuit to have a gain of 40 would be,
Rin = 10KΩ and Rf = 400KΩ.
The formula could also be rearranged to give a new value of Rin, keeping the same value of Rf.
One final point to note about the Inverting Amplifier configuration for an operational amplifier, if the two resistors are of equal value, Rin = Rf then the gain of the amplifier will be -1 producing a complementary form of the input voltage at its output as Vout = -Vin. This type of inverting amplifier configuration is generally called a Unity Gain Inverter of simply an Inverting Buffer.
The Non-inverting Amplifier
The second basic configuration of an operational amplifier circuit is that of a Non-inverting Amplifier. In this configuration, the input voltage signal, (Vin) is applied directly to the non-inverting (+) input terminal which means that the output gain of the amplifier becomes "Positive" in value in contrast to the "Inverting Amplifier" circuit we saw in the last tutorial whose output gain is negative in value. The result of this is that the output signal is "in-phase" with the input signal.
Feedback control of the non-inverting amplifier is achieved by applying a small part of the output voltage signal back to the inverting (-) input terminal via a Rf - R2 voltage divider network, again producing negative feedback. This closed-loop configuration produces a non-inverting amplifier circuit with very good stability, a very high input impedance, Rin approaching infinity, as no current flows into the positive input terminal, (ideal conditions) and a low output impedance, Rout as shown below.
Non-inverting Amplifier Configuration
In the previous Inverting Amplifier tutorial, we said that "no current flows into the input" of the amplifier and that "V1 equals V2". This was because the junction of the input and feedback signal (V1) are at the same potential in other words the junction is a "virtual earth" summing point. Because of this virtual earth node the resistors, Rf and R2 form a simple potential divider network across the non-inverting amplifier with the voltage gain of the circuit being determined by the ratios of R2 and Rf as shown below.
Equivalent Potential Divider Network
Then using the formula to calculate the output voltage of a potential divider network, we can calculate the closed-loop voltage gain (Av) of the Non-inverting Amplifier as follows:
Then the closed loop voltage gain of a Non-inverting Amplifier is given as:
We can see from the equation above, that the overall closed-loop gain of a non-inverting amplifier will always be greater but never less than one (unity), it is positive in nature and is determined by the ratio of the values of Rf and R2. If the value of the feedback resistor Rf is zero, the gain of the amplifier will be exactly equal to one (unity). If resistor R2 is zero the gain will approach infinity, but in practice it will be limited to the operational amplifiers open-loop differential gain, (Ao).
We can easily convert an inverting operational amplifier configuration into a non-inverting amplifier configuration by simply changing the input connections as shown.
Voltage Follower (Unity Gain Buffer)
If we made the feedback resistor, Rf equal to zero, (Rf = 0), and resistor R2 equal to infinity, (R2 = ∞), then the circuit would have a fixed gain of "1" as all the output voltage would be present on the inverting input terminal (negative feedback). This would then produce a special type of the non-inverting amplifier circuit called a Voltage Follower or also called a "unity gain buffer".
As the input signal is connected directly to the non-inverting input of the amplifier the output signal is not inverted resulting in the output voltage being equal to the input voltage, Vout = Vin. This then makes thevoltage follower circuit ideal as a Unity Gain Buffer circuit because of its isolation properties as impedance or circuit isolation is more important than amplification while maintaining the signal voltage. The input impedance of the voltage follower circuit is very high, typically above 1MΩ as it is equal to that of the operational amplifiers input resistance times its gain (Rin x Ao). Also its output impedance is very low since an ideal op-amp condition is assumed.
 |
| Voltage Follower |
In this non-inverting circuit configuration, the input impedance Rin has increased to infinity and the feedback impedance Rf reduced to zero. The output is connected directly back to the negative inverting input so the feedback is 100% and Vin is exactly equal to Vout giving it a fixed gain of 1 or unity. As the input voltage Vin is applied to the non-inverting input the gain of the amplifier is given as:
Since no current flows into the non-inverting input terminal the input impedance is infinite (ideal op-amp) and also no current flows through the feedback loop so any value of resistance may be placed in the feedback loop without affecting the characteristics of the circuit as no voltage is dissipated across it, zero current flows, zero voltage drop, zero power loss. Since the input current is zero giving zero input power, the voltage follower can provide a large power gain. However in most real unity gain buffer circuits a low value (typically 1kΩ) resistor is required to reduce any offset input leakage currents, and also if the operational amplifier is of a current feedback type.
The voltage follower or unity gain buffer is a special and very useful type of Non-inverting amplifiercircuit that is commonly used in electronics to isolated circuits from each other especially in High-order state variable or Sallen-Key type active filters to separate one filter stage from the other. Typical digital buffer IC's available are the 74LS125 Quad 3-state buffer or the more common 74LS244 Octal buffer.
One final thought, the output voltage gain of the voltage follower circuit with closed loop gain is Unity, the voltage gain of an ideal operational amplifier with open loop gain (no feedback) is Infinite. Then by carefully selecting the feedback components we can control the amount of gain produced by an operational amplifier anywhere from one to infinity.
Thus far we have analysed an inverting and non-inverting amplifier circuit that has just one input signal,Vin.
The Summing Amplifier
The Summing Amplifier is a very flexible circuit based upon the standard Inverting Operational Amplifierconfiguration that can be used for combining multiple inputs. We saw previously in the inverting amplifier tutorial that the inverting amplifier has a single input voltage, (Vin) applied to the inverting input terminal. If we add more input resistors to the input, each equal in value to the original input resistor, Rinwe end up with another operational amplifier circuit called a Summing Amplifier, "summing inverter" or even a "voltage adder" circuit as shown below.
Summing Amplifier Circuit
The output voltage, (Vout) now becomes proportional to the sum of the input voltages, V1, V2, V3 etc. Then we can modify the original equation for the inverting amplifier to take account of these new inputs thus:
However, if all the input impedances, (Rin) are equal in value the final equation for the output voltage is given as:
Summing Amplifier Equation
We now have an operational amplifier circuit that will amplify each individual input voltage and produce an output voltage signal that is proportional to the algebraic "SUM" of the three individual input voltagesV1, V2 and V3. We can also add more inputs if required as each individual input "see's" their respective resistance, Rin as the only input impedance. This is because the input signals are effectively isolated from each other by the "virtual earth" node at the inverting input of the op-amp. A direct voltage addition can also be obtained when all the resistances are of equal value and Rf is equal to Rin.
A Scaling Summing Amplifier can be made if the individual input resistors are "NOT" equal. Then the equation would have to be modified to:
To make the math's a little easier, we can rearrange the above formula to make the feedback resistorRF the subject of the equation giving the output voltage as:
This allows the output voltage to be easily calculated if more input resistors are connected to the amplifiers inverting input terminal. The input impedance of each individual channel is the value of their respective input resistors, ie, R1, R2, R3 ... etc.
The Summing Amplifier is a very flexible circuit indeed, enabling us to effectively "Add" or "Sum" together several individual input signals. If the inputs resistors, R1, R2, R3 etc, are all equal a unity gain inverting adder can be made. However, if the input resistors are of different values a "scaling summing amplifier" is produced which gives a weighted sum of the input signals.
Example No1
Find the output voltage of the following Summing Amplifier circuit.
Summing Amplifier
Using the previously found formula for the gain of the circuit
we can now substitute the values of the resistors in the circuit as follows,
then the output voltage of the Summing Amplifier circuit above is given as -45 mV and is negative as its an inverting amplifier.
Summing Amplifier Applications
If the input resistances of a summing amplifier are connected to potentiometers the individual input signals can be mixed together by varying amounts. For example, measuring temperature, you could add a negative offset voltage to make the display read "0" at the freezing point or produce an audio mixer for adding or mixing together individual waveforms (sounds) from different source channels (vocals, instruments, etc) before sending them combined to an audio amplifier.
Summing Amplifier Audio Mixer
Another useful application of a Summing Amplifier is as a weighted sum digital-to-analogue converter. If the input resistors, Rin of the summing amplifier double in value for each input, for example, 1kΩ, 2kΩ, 4kΩ, 8kΩ, 16kΩ, etc, then a digital logical voltage, either a logic level "0" or a logic level "1" on these inputs will produce an output which is the weighted sum of the digital inputs. Consider the circuit below.
Digital to Analogue Converter
Of course this is a simple example. In this DAC summing amplifier circuit, the number of individual bits that make up the input data word, and in this example 4-bits, will ultimately determine the output step voltage as a percentage of the full-scale analogue output voltage. Also, the accuracy of this full-scale analogue output depends on voltage levels of the input bits being consistently 0V for "0" and consistently 5V for "1" as well as the accuracy of the resistance values used for the input resistors, Rin. Fortunately to overcome these errors, commercial available Digital-to Analogue and Analogue-to Digital devices are available.
Differential Amplifier
Thus far we have used only one of the operational amplifiers inputs to connect to the amplifier, using either the "inverting" or the "non-inverting" input terminal to amplify a single input signal with the other input being connected to ground. But we can also connect signals to both of the inputs at the same time producing another common type of operational amplifier circuit called a Differential Amplifier.
Basically, as we saw in the first tutorial about operational amplifiers, all op-amps are "Differential Amplifiers" due to their input configuration. But by connecting one voltage signal onto one input terminal and another voltage signal onto the other input terminal the resultant output voltage will be proportional to the "Difference" between the two input voltage signals of V1 and V2. Then differential amplifiers amplify the difference between two voltages making this type of circuit a Subtractor unlike a summing amplifier which adds or sums together the input voltages. This type of operational amplifier circuit is commonly known as a Differential Amplifier configuration and is shown below:
Differential Amplifier
By connecting each input inturn to 0v ground we can use superposition to solve for the output voltageVout. Then the transfer function for a Differential Amplifier circuit is given as:
When resistors, R1 = R2 and R3 = R4 the above transfer function for the differential amplifier can be simplified to the following expression:
Differential Amplifier Equation
If all the resistors are all of the same ohmic value, that is: R1 = R2 = R3 = R4 then the circuit will become a Unity Gain Differential Amplifier and the voltage gain of the amplifier will be exactly one or unity. Then the output expression would simply be Vout = V2 - V1.
The Differential Amplifier circuit is a very useful op-amp circuit and by adding more resistors in parallel with the input resistors R1 and R3, the resultant circuit can be made to either "Add" or "Subtract" the voltages applied to their respective inputs. One of the most common ways of doing this is to connect a "Resistive Bridge" commonly called a Wheatstone Bridge to the input of the amplifier as shown below.
Bridge Amplifier
The standard Differential Amplifier circuit now becomes a differential voltage comparator by "Comparing" one input voltage to the other. For example, by connecting one input to a fixed voltage reference set up on one leg of the resistive bridge network and the other to either a "Thermistor" or a "Light Dependant Resistor" the amplifier circuit can be used to detect either low or high levels of temperature or light as the output voltage becomes a linear function of the changes in the active leg of the resistive bridge and this is demonstrated below.
Light Activated Switch
Here the circuit above acts as a light-activated switch which turns the output relay either "ON" or "OFF" as the light level detected by the LDR resistor exceeds or falls below a pre-set value at V2 determined by the position of VR1. A fixed voltage reference is applied to the inverting input terminal V1 via the R1 - R2 voltage divider network and the variable voltage (proportional to the light level) applied to the non-inverting input terminal V2. It is also possible to detect temperature using this type of circuit by simply replacing the Light Dependant Resistor (LDR) with a thermistor. By interchanging the positions of VR1and the LDR, the circuit can be used to detect either light or dark, or heat or cold using a thermistor.
One major limitation of this type of amplifier design is that its input impedances are lower compared to that of other operational amplifier configurations, for example, a non-inverting (single-ended input) amplifier. Each input voltage source has to drive current through an input resistance, which has less overall impedance than that of the op-amps input alone. This may be good for a low impedance source such as the bridge circuit above, but not so good for a high impedance source.
One way to overcome this problem is to add a Unity Gain Buffer Amplifier such as the voltage follower seen in the previous tutorial to each input resistor. This then gives us a differential amplifier circuit with very high input impedance and low output impedance as it consists of two non-inverting buffers and one differential amplifier. This then forms the basis for most "Instrumentation Amplifiers".
Instrumentation Amplifier
Instrumentation Amplifiers (in-amps) are very high gain differential amplifiers which have a high input impedance and a single ended output. Instrumentation amplifiers are mainly used to amplify very small differential signals from strain gauges, thermocouples or current sensing devices in motor control systems. Unlike standard operational amplifiers in which their closed-loop gain is determined by an external resistive feedback connected between their output terminal and one input terminal, either positive or negative, instrumentation amplifiers have an internal feedback resistor that is effectively isolated from its input terminals as the input signal is applied across two differential inputs, V1 and V2.
The instrumentation amplifier also has a very good common mode rejection ratio, CMRR (zero output when V1 = V2) well in excess of 100dB at DC. A typical example of a three op-amp instrumentation amplifier with a high input impedance (Zin) is given below:
High Input Impedance Instrumentation Amplifier
The two non-inverting amplifiers form a differential input stage acting as buffer amplifiers with a gain of1 + 2R2/R1 for differential input signals and unity gain for common mode input signals. Since amplifiers A1 and A2 are closed loop negative feedback amplifiers, we can expect the voltage at Va to be equal to the input voltage V1. Likewise, the voltage at Vb to be equal to the value at V2.
As the op-amps take no current at their input terminals (virtual earth), the same current must flow through the three resistor network of R2, R1 and R2 connected across the op-amp outputs. This means then that the voltage on the upper end of R1 will be equal to V1 and the voltage at the lower end of R1 to be equal to V2. This produces a voltage drop across resistor R1 which is equal to the voltage difference between inputs V1 and V2, the differential input voltage, because the voltage at the summing junction of each amplifier, Va and Vb is equal to the voltage applied to its positive inputs.
However, if a common-mode voltage is applied to the amplifiers inputs, the voltages on each side of R1will be equal, and no current will flow through this resistor. Since no current flows through R1 (nor, therefore, through both R2 resistors, amplifiers A1 and A2 will operate as unity-gain followers (buffers). Since the input voltage at the outputs of amplifiers A1 and A2 appears differentially across the three resistor network, the differential gain of the circuit can be varied by just changing the value of R1.
The voltage output from the differential op-amp A3 acting as a subtractor, is simply the difference between its two inputs (V2 - V1) and which is amplified by the gain of A3 which may be one, unity, (assuming that R3 = R4). Then we have a general expression for overall voltage gain of the instrumentation amplifier circuit as:
Instrumentation Amplifier Equation
In the next tutorial about Operational Amplifiers, we will examine the effect of the output voltage, Voutwhen the feedback resistor is replaced with a frequency dependant reactance in the form of a capacitance. The addition of this feedback capacitance produces a non-linear operational amplifier circuit called an Integrating Amplifier
The Op-amp Integrator Amplifier
In the previous tutorials we have seen circuits which show how an operational amplifier can be used as part of a positive or negative feedback amplifier or as an adder or subtractor type circuit using just pure resistances in both the input and the feedback loop. But what if we were to change the purely resistive (Rf) feedback element of an inverting amplifier to that of a frequency dependant impedance, (Z) type complex element, such as a Capacitor, C. What would be the effect on the output voltage. By replacing this feedback resistance with a capacitor we now have an RC Network across the operational amplifier producing an Op-amp Integrator circuit as shown below.
Op-amp Integrator Circuit
As its name implies, the Op-amp Integrator is an operational amplifier circuit that performs the mathematical operation of Integration, that is we can cause the output to respond to changes in the input voltage over time. The integrator amplifier acts like a storage element that "produces a voltage output which is proportional to the integral of its input voltage with respect to time". In other words the magnitude of the output signal is determined by the length of time a voltage is present at its input as the current through the feedback loop charges or discharges the capacitor as the required negative feedback occurs through the capacitor.
When a voltage, Vin is firstly applied to the input of an integrating amplifier, the uncharged capacitor Chas very little resistance and acts a bit like a short circuit (voltage follower circuit) giving an overall gain of less than one. No current flows into the amplifiers input and point X is a virtual earth resulting in zero output. As the feedback capacitor C begins to charge up, its reactance Xc decreases this results in the ratio of Xc/Rin increasing producing an output voltage that continues to increase until the capacitor is fully charged.
At this point the capacitor acts as an open circuit, blocking anymore flow of DC current. The ratio of feedback capacitor to input resistor (Xc/Rin) is now infinite resulting in infinite gain. The result of this high gain (similar to the op-amps open-loop gain), is that the output of the amplifier goes into saturation as shown below. (Saturation occurs when the output voltage of the amplifier swings heavily to one voltage supply rail or the other with little or no control in between).
The rate at which the output voltage increases (the rate of change) is determined by the value of the resistor and the capacitor, "RC time constant". By changing this RC time constant value, either by changing the value of the Capacitor, C or the Resistor, R, the time in which it takes the output voltage to reach saturation can also be changed for example.
If we apply a constantly changing input signal such as a square wave to the input of an Integrator Amplifier then the capacitor will charge and discharge in response to changes in the input signal. This results in the output signal being that of a sawtooth waveform whose frequency is dependant upon theRC time constant of the resistor/capacitor combination. This type of circuit is also known as a Ramp Generator and the transfer function is given below.
Ramp Generator
We know from first principals that the voltage on the plates of a capacitor is equal to the charge on the capacitor divided by its capacitance giving Q/C. Then the voltage across the capacitor is output Vouttherefore: -Vout = Q/C. If the capacitor is charging and discharging, the rate of charge of voltage across the capacitor is given as:
But dQ/dt is electric current and since the node voltage of the integrating op-amp at its inverting input terminal is zero, X = 0, the input current I(in) flowing through the input resistor, Rin is given as:
The current flowing through the feedback capacitor C is given as:
Assuming that the input impedance of the op-amp is infinite (ideal op-amp), no current flows into the op-amp terminal. Therefore, the nodal equation at the inverting input terminal is given as:
From which we derive an ideal voltage output for the OP-amp Integrator as:
To simplify the math's a little, this can also be re-written as:
Where jω = 2πƒ and the output voltage Vout is a constant 1/RC times the integral of the input voltageVin with respect to time. The minus sign (-) indicates a 180o phase shift because the input signal is connected directly to the inverting input terminal of the op-amp.
The AC or Continuous Op-amp Integrator
If we changed the above square wave input signal to that of a sine wave of varying frequency the Op-amp Integrator performs less like an integrator and begins to behave more like an active "Low Pass Filter", passing low frequency signals while attenuating the high frequencies. At 0Hz or DC, the capacitor acts like an open circuit blocking any feedback voltage resulting in very little negative feedback from the output back to the input of the amplifier. Then with just the feedback capacitor, C, the amplifier effectively is connected as a normal open-loop amplifier which has very high open-loop gain resulting in the output voltage saturating.
This circuit connects a high value resistance in parallel with a continuously charging and discharging capacitor. The addition of this feedback resistor, R2 across the capacitor, C gives the circuit the characteristics of an inverting amplifier with finite closed-loop gain of R2/R1 at very low frequencies while acting as an integrator at higher frequencies has the capacitor shorts out the feedback resistor,R2.
The AC Op-amp Integrator with DC Gain Control
Unlike the DC integrator amplifier above whose output voltage at any instant will be the integral of a waveform so that when the input is a square wave, the output waveform will be triangular. For an AC integrator, a sinusoidal input waveform will produce another sine wave as its output which will be 90oout-of-phase with the input producing a cosine wave. Further more, when the input is triangular, the output waveform is also sinusoidal. This then forms the basis of a Active Low Pass Filter as seen before in the filters section tutorials with a corner frequency given as.
In the next tutorial about Operational Amplifiers, we will analyse the complement of the Op-amp Integrator operational amplifier circuit called the Differentiator Amplifier that produces an output signal which is the mathematical operation of differentiation, that is it produces a voltage output which is proportional to the input voltage's rate-of-change and the current flowing through the input capacitor..
The Op-amp Differentiator Amplifier
The basic Op-amp Differentiator circuit is the exact opposite to that of the Integrator operational amplifier circuit that we saw in the previous tutorial. Here, the position of the capacitor and resistor have been reversed and now the reactance, Xc is connected to the input terminal of the inverting amplifier while the resistor, Rf forms the negative feedback element across the operational amplifier as normal.
This circuit performs the mathematical operation of Differentiation, that is it "produces a voltage output which is directly proportional to the input voltage's rate-of-change with respect to time". In other words the faster or larger the change to the input voltage signal, the greater the input current, the greater will be the output voltage change in response, becoming more of a "spike" in shape.
As with the integrator circuit, we have a resistor and capacitor forming an RC Network across the operational amplifier and the reactance (Xc) of the capacitor plays a major role in the performance of aOp-amp Differentiator.
Op-amp Differentiator Circuit
The input signal to the differentiator is applied to the capacitor. The capacitor blocks any DC content so there is no current flow to the amplifier summing point, X resulting in zero output voltage. The capacitor only allows AC type input voltage changes to pass through and whose frequency is dependant on the rate of change of the input signal. At low frequencies the reactance of the capacitor is "High" resulting in a low gain (Rf/Xc) and low output voltage from the op-amp. At higher frequencies the reactance of the capacitor is much lower resulting in a higher gain and higher output voltage from the differentiator amplifier.
However, at high frequencies an op-amp differentiator circuit becomes unstable and will start to oscillate. This is due mainly to the first-order effect, which determines the frequency response of the op-amp circuit causing a second-order response which, at high frequencies gives an output voltage far higher than what would be expected. To avoid this the high frequency gain of the circuit needs to be reduced by adding an additional small value capacitor across the feedback resistor Rf.
Ok, some math's to explain what's going on!. Since the node voltage of the operational amplifier at its inverting input terminal is zero, the current, i flowing through the capacitor will be given as:
The charge on the capacitor equals Capacitance x Voltage across the capacitor
The rate of change of this charge is
but dQ/dt is the capacitor current i
from which we have an ideal voltage output for the op-amp differentiator is given as:
Therefore, the output voltage Vout is a constant -Rf.C times the derivative of the input voltage Vin with respect to time. The minus sign indicates a 180o phase shift because the input signal is connected to the inverting input terminal of the operational amplifier.
One final point to mention, the Op-amp Differentiator circuit in its basic form has two main disadvantages compared to the previous integrator circuit. One is that it suffers from instability at high frequencies as mentioned above, and the other is that the capacitive input makes it very susceptible to random noise signals and any noise or harmonics present in the source circuit will be amplified more than the input signal itself. This is because the output is proportional to the slope of the input voltage so some means of limiting the bandwidth in order to achieve closed-loop stability is required
Op-amp Differentiator Waveforms
If we apply a constantly changing signal such as a Square-wave, Triangular or Sine-wave type signal to the input of a differentiator amplifier circuit the resultant output signal will be changed and whose final shape is dependant upon the RC time constant of the Resistor/Capacitor combination.
Improved Op-amp Differentiator Amplifier
The basic single resistor and single capacitor op-amp differentiator circuit is not widely used to reform the mathematical function of Differentiation because of the two inherent faults mentioned above, "Instability" and "Noise". So in order to reduce the overall closed-loop gain of the circuit at high frequencies, an extra resistor, Rin is added to the input as shown below.
Improved Op-amp Differentiator Amplifier Circuit
Adding the input resistor Rin limits the differentiators increase in gain at a ratio of Rf/Rin. The circuit now acts like a differentiator amplifier at low frequencies and an amplifier with resistive feedback at high frequencies giving much better noise rejection. Additional attenuation of higher frequencies is accomplished by connecting a capacitor C1 in parallel with the differentiator feedback resistor, Rf. This then forms the basis of a Active High Pass Filter as we have seen before in the filters section.
Operational Amplifiers Summary
The following is a summary of the different types of Operational Amplifiers and their configurations discussed in this tutorial section.
- The Operational Amplifier, or Op-amp as it is most commonly called, is an ideal amplifier with infinite Gain and Bandwidth when used in the Open-loop mode with typical d.c. gains of well over 100,000, or 100dB.
- The basic Op-amp construction is of a 3-terminal device, 2-inputs and 1-output.
- An Operational Amplifier operates from either a dual positive ( +V ) and an corresponding negative ( -V ) supply, or they can operate from a single DC supply voltage.
- The two main laws associated with the operational amplifier are that it has an infinite input impedance, ( Z∞ ) resulting in "No current flowing into either of its two inputs" and zero input offset voltage "V1 = V2".
- An operational amplifier also has zero output impedance, ( Z = 0 ).
- Op-amps sense the difference between the voltage signals applied to their two input terminals and then multiply it by some pre-determined Gain, ( A ).
- This Gain, ( A ) is often referred to as the amplifiers "Open-loop Gain".
- Closing the open loop by connecting a resistive or reactive component between the output and one input terminal of the op-amp greatly reduces and controls this open-loop gain.
- Op-amps can be connected into two basic configurations, Inverting and Non-inverting.
The Two Basic Operational Amplifier Circuits
The Open-loop gain called the Gain Bandwidth Product, or (GBP) can be very high and is a measure of how good an amplifier is.- Very high GBP makes an operational amplifier circuit unstable as a micro volt input signal causes the output voltage to swing into saturation.
- By the use of a suitable feedback resistor, ( Rf ) the overall gain of the amplifier can be accurately controlled.
Gain Bandwidth Product
- For negative feedback, were the fed-back voltage is in "anti-phase" to the input the overall gain of the amplifier is reduced.
- For positive feedback, were the fed-back voltage is in "Phase" with the input the overall gain of the amplifier is increased.
- By connecting the output directly back to the negative input terminal, 100% feedback is achieved resulting in a Voltage Follower (buffer) circuit with a constant gain of 1 (Unity).
- Changing the fixed feedback resistor ( Rf ) for a Potentiometer, the circuit will have Adjustable Gain.
- The Differential Amplifier produces an output that is proportional to the difference between the 2 input voltages.
Differential and Summing Operational Amplifier Circuits
Adding more input resistor to either the inverting or non-inverting inputs Voltage Adders orSummers can be made.- Voltage follower op-amps can be added to the inputs of Differential amplifiers to produce high impedance Instrumentation amplifiers.
- The Integrator Amplifier produces an output that is the mathematical operation of integration.
- The Differentiator Amplifier produces an output that is the mathematical operation of differentiation.
- Both the Integrator and Differentiator Amplifiers have a resistor and capacitor connected across the op-amp and are affected by its RC time constant.
- In their basic form, Differentiator Amplifiers suffer from instability and noise but additional components can be added to reduce the overall closed-loop gain.
Differentiator and Integrator Operational Amplifier Circuits
